如何设计正交实验?正交方案是怎么设计的?正交实验设计当析因设计需要过多的实验时,从析因设计的水平组合中选择一些有代表性的水平组合进行实验是一个非常自然的想法。正交实验设计的依据是什么?正交试验设计是研究多因素多水平的另一种设计方法,它根据正交性从综合实验中选取一些代表点,这些代表点具有“均匀分散、均匀可比”的特点,正交试验设计是部分因子设计的主要方法。

正交实验设计当析因设计需要过多的实验时,从析因设计的水平组合中选取一些有代表性的水平组合进行实验是非常自然的想法。因此,部分因子设计是存在的,但对于缺乏实验设计知识的实际工作者来说,选择一个合适的部分因子设计仍然是困难的。正交试验设计是研究多因素多水平的另一种设计方法。它根据正交性从综合实验中选取一些代表点,这些代表点具有“均匀分散、均匀可比”的特点。正交试验设计是部分因子设计的主要方法。
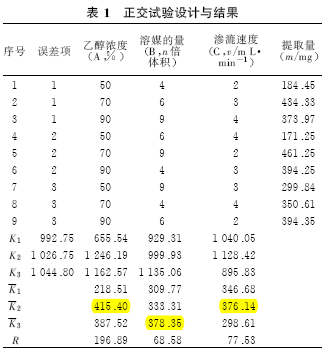
日本著名统计学家田口健一把正交试验选出的水平组合列在一个表中,称为正交表。比如做一个三因素三水平的实验,按照综合实验的要求,必须进行3327个实验组合,还没有考虑每个组合的重复次数。如果按照L9(3)3正交表安排实验,只需要9个实验,按照L18(3)7正交表进行18个实验,显然大大减少了工作量。

就像在优化区域放一个网格,如果互联网上的每一个点都被测试;正方体每条线上刚好有一个测试点,三个因素的优化区域可以用一个正方体来表示(图122),这在动物实验中是不可能的。正交设计是从最优选择区域的综合实验点(水平组合)中选择一些有代表性的实验点(水平组合)进行实验。在立方体的每个平面上,正好有三个实验点,非常具有代表性。(2)正交设计的基本原则在实验安排上,每个因素在研究范围内选取几个水平,这就是综合实验。

2。最长距离法将类之间的距离定义为彼此相距最远的两个事例之间的距离。最长距离法克服了最短距离法的缺点,合并后两个类与其他类的距离最大,增加了合并后的类与其他类的距离。3.平均连接法,最短最长距离法只利用两个事例之间的距离来确定两个类之间的距离。
有将方差小的类进行聚类的倾向,效果好,应用广泛。4.重心法将两个类之间的距离定义为两个类的重心之间的距离,每个类的重心是每个变量中所有情况的平均值所代表的点。与上述三类不同的是,重心法每次合并都需要重新计算。也较少受到特殊点的影响。重心法要求欧氏距离,其主要缺点在聚类过程中。
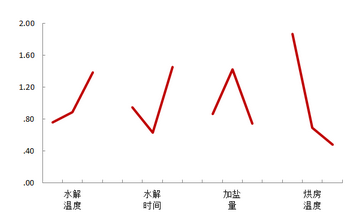
实验原理酶的催化是在一定条件下进行的,受多种因素影响,如底物浓度、酶浓度、溶液的pH值和离子浓度、温度、抑制剂和激活剂等。通常在其他因素不变的情况下,通过测定某一因素在一系列变化条件下的酶活来得出某一因素对酶活的影响,这是一种简单的单因素比较法。本实验采用正交法,即多因素(≥3)实验方法,确定了温度、pH值、底物浓度和酶浓度对转化酶活性的影响。

扩展数据:正交试验法的步骤如下:1 .确定测试的目的。实验的目的多种多样,如寻找产品质量指标的最佳组合,确定最佳工艺条件等。这个实验的目的是提高酶的反应速度和活性。2.选择质量特性指标。应选择可以改进或提高的质量特性和因素效应。对于这个实验,它是产生的产物(葡萄糖)的量。3.选择相关因素。
一般先确定实验的因素、水平和交互作用,再选择适用的L表。在确定因素的层次数时,主要因素应安排在较多层次上,次要因素可安排在较少层次上。(1)先看级别号。如果所有因素都是2水平,选择L (2 *)表;如果所有因素都是3级,则选择L (3 *)表。如果每个因素的水平不同,选择适当的混合水平表。(2)每次交互应在正交表中占据一列或两列。
为了分析测试结果的方差或回归,必须至少留下一个空白列作为“误差”列,该列应被视为范围分析中的“其他因素”列。(3)取决于测试精度的要求。如果要求高,就要考实验多的L表。(4)如果试验费用昂贵,或试验经费有限,或人力、时间紧张,则不宜选择试验过多的L表。(5)根据最初考虑的因素、水平和交互作用选择正交表。如果没有正交表可供选择,简单可行的办法就是适当修改原水平数。
考虑一个三因素实验,每个因素有三个水平。如果做一个全面的测试,需要3 327次。图:正交实验设计示意图如果从27个实验中选取一些实验,A和B往往分别固定在A1和B1水平,与C、A1B1C1、A1B1C2和A1B1C3三个水平相匹配。经过这三个测试,如果A1B1C3是最好的,那么就以C3为等级,让A1和C3固定,再搭配因子B的三个等级,A1B2C3,
经过这两个实验,如果A1B2C3最好,那我们就把B2和C3作为两个水平,再做两个实验A2B2C3,A3B2C3,然后相互比较。如果A3B2C3是最好的,那么我们可以得出结论,A3B2C3是我们想要选择的最佳水平组合。这样,仅经过7次测试就选出了最佳水平组合。我们发现这些测试结果都分布在立方体的角上,不具有代表性,所以用上述方法选出的测试水平组合并不是真正的最佳组合。
当析因设计需要过多的实验时,从实验设计的水平组合中选取一些有代表性的水平组合进行实验是一个非常自然的想法。因此,部分因子设计是存在的,但对于缺乏实验设计知识的实际工作者来说,选择一个合适的部分因子设计仍然是困难的。正交试验设计是研究多因素多水平的另一种设计方法。它根据正交性从综合实验中选取一些代表点,这些代表点具有“均匀分散、均匀可比”的特点。正交试验设计是部分因子设计的主要方法。
日本著名统计学家田口健一把正交试验选出的水平组合列在一个表中,称为正交表。比如做一个三因素三水平的实验,按照综合实验的要求,必须进行3327个实验组合,还没有考虑每个组合的重复次数。如果按照L9(3)3正交表安排实验,只需要9个实验,按照L18(3)7正交表进行18个实验,显然大大减少了工作量。
正交试验设计法是研究和处理多因素试验的科学方法。它最早于20世纪20年代在英国罗伦斯特农业实验站产生(侯等,1985),后由日本田口野一博士于50年代编制了正交实验表,60年代初从日本传入中国。它根据伽罗瓦理论推导出的正交表,从大量的实验条件中选择合适的、有代表性的条件来合理安排实验,被称为国际标准的正交实验法。
下面只简单介绍第一种正交表,其一般符号可以表示为:Ln(ji): l正交表符号;n正交表的行数(实验或实验方案数);正交表中的j数(因子的水平数或标度系列);I正交表中的列数(实验因素数)。例如,一个工厂想提高某种产品的质量或产量,对过程中的三个主要因素在三个水平上进行实验(表5.1),寻找最合适的操作条件。

